ELS
Dimensionner à l'ELS revient à comparer la Déformée d'un élément à une Déformée limite
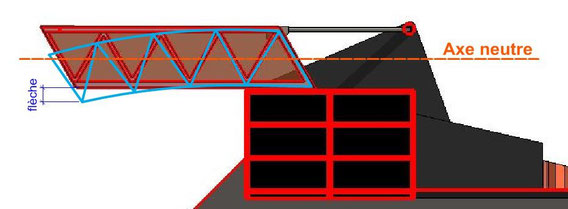
En service, la structure de notre bâtiment pont ne doit pas trop se déformer.
Nous allons limiter la flèche à une valeur admissible.
Vérifions que la déformée de la poutre treillis dimensionnée à l'ELU est acceptable
L'objectif est donc de déterminer la flèche maximale de nos poutres treillis constituées de sections pleines en acier de 86 m de côté.
Nous limiterons la flèche au 1/300° soit 24800 mm / 300 = 83 mm
Données:
- la poutre fait 24.8 m de long
- l'entre-axe entre les semelles sup et inf des deux poutres treillis = 8.8 m - 0.1 m = 8.7 m
- la charge linéaire majorée (ELS) calculée précédemment est de 90.2/2 = 45.1 kN/m par poutre treillis
Comment calculer la flèche d'une poutre encastrée?
Pour calculer une flèche, nous avons besoins de notions théoriques préalables.
Nous allons donc faire un détour par ces différentes notions:
1- Relation entre contrainte et moment par la formule d'équarrissage
2- Exploration de la notion d'Inertie
3- Détermination de la flèche admissible
La flèche maximale d'une poutre encastrée-libre est égale à:
f = ...
Déterminons une flèche admissible
Nous prendrons de manière classique une flèche maximale admissible de 1/300°
Soit 24.8 m / 300 = 8.3 cm
Calculons la flèche de notre poutre treillis composées de profilés carrés pleins de 10 cm de côté
f = pl^4 / (8EI)
E = 10 000 N/mm²
pl = 90.2/2 = 45.1 kN/m
I = bh^3/12 - bh'^3/12
Avec:
b = la hauteur du bâtiment: 880 cm dans notre cas
b' = b - 2xH(profilé) = la distance qui sépare les profilés des semelles sup et inf = 880 - 2x10
= 860 cm
La flèche de ces poutres treillis est-elle acceptable?
Changeons les poutres treillis par des poutres en lamellé-collé