Quelle est le rôle du tirant métallique?
1- empécher le basculement vers l'avant du bâtiment-pont. Il doit donc être capable de résister au poids de celui-ci.
2- empécher que son allongement ne fasse trop pencher le bâtiment-pont vers l'avant.
Commençons par le rôle le plus important: résister au basculement vers l'avant du bâtiment-pont: une question de RESISTANCE
Pour déterminer la section d'acier nécessaire pour reprendre les effort:
- nous devons connaitre l'effort dans le tirant
- nous devons connaitre la résistance d'un tirant en acier d'une section donnée.

Comment déterminer l'effort dans le câble?
Déterminons l'effort dans le tirant
L'effort que le tirant va subir est de la traction. C'est un EFFORT INTERNE ou SOLLICIATION que nous noterons N.
Cette solliciation est provoquée par la charge du bâtiment: le poids propre de celui-ci et les charges d'utilisations, c'est à dire les charges qu'il est sensé supporter (les gens, le mobilier,...). Ces charges sont des EFFORTS EXTERNES (elles sont "externes" à la structure) ou ACTIONS.
Nous reviendrons ultérieurement plus en détail sur les ACTIONS.

Le tirant est soumis à un effort de traction parallèle à son axe. Nous notons cette sollicitation N.
N est aussi égale en grandeur à la réaction d'appui du second appui que nous venons de créer en ajoutant ce hauban.
N est donc dû à la charge du bâtiment soutenue par le tirant.

Comment déterminer N?
Principe d'équilibre (rappel)
Comme N est égale en grandeur à la Réaction de l'appui 2, il suffit de déterminer cette réaction d'appui grâce au PRINCIPE D'EQUILIBRE.
Celui-ci nous dit que l'ensemble des ACTIONS (forces et moments) qui agissent sur un solide au repos (sans accélération) a une résultante nulle.
Somme des F = 0
Somme des M = 0

Représentons le bâtiment-pont en exprimant les réactions d'appui.
Charge linéaire "pl"
Ces réactions d'appui existent à cause du "poids" du bâtiment (qui est l'action)
Le bâtiment ayant une largeur constante, nous allons exprimer ce "poids" sous la forme d'une charge linéaire "pl" constante sur toute la longueur de celui-ci.
Imaginons que cellui-ci "pèse" un total de 350 tonnes.
Alors la charge linéaire pl vaut:
= 350 tonnes / 34.64 m = 10 tonnes / m
Unités de la norme
1 kgf = 10 N (environ)
En fonction de la norme actuelle, nous parlerons de kN (et non plus de tonnes, de kg).
Si donc la masse de notre bâtiment est de 3500 kN (= à peu de choses près 350 tonnes)
Alors nous écrirons que la charge linéaire pl vaut:
3500 kN / 34.64 m = 100 kN / m (environ)
Déterminons les réactions d'appui à partir des relations d'équilibre
Sommes des Forces Horizontales = 0
0 = R1h + R2h
-> R1h = - R2h
Sommes des Forces Verticales = 0
0 = R1v + R2v - pl x L
-> R1v = - R2v + pl x L
Somme des Moments = 0
Autour de l'appui 2:
0 = (34.6 m x pl) x 34.6/2 m - R1v x 24.8 m
-> R1v = (34.6m)²/(24.8mx2) x pl = pl x 24.14m
-> R2v = - R1v + pl x 34.6m = pl x (34.6m - 24.14m) = pl x 10.46m
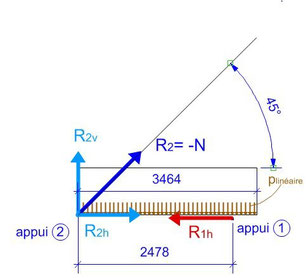
Notre schéma se simplifie donc en ceci.
De plus, comme le tirant est à 45°:
R2v / N = sinus 45°
Pour déterminer N, nous devons connaitre pl.
Que vaut la charge réelle du bâtiment ramenée par unité de longueur?
Comment déterminer pl? Etape 1: déterminer les charges surfacique (par m²)
Les charges reprisent par le bâtiment se divisent en deux grandes familles:
1- les charges PERMANENTES telles que le poids propre, les cloisons, ... tout ce qui est fixé au bâtiment
2- les charges VARIABLES ou CHARGES D'EXPOITATION telles que le mobilier, les gens, le vent ...
Nous allons simplifier et considérer (ce qui est proche de la réalité) que toutes ces charges sont surfaciques: elles se comptent par mètre carré de plancher. Nous parlerons plus loin d'autres types de charges (non surfaciques).
Nous allons également considérer que dans notre bâtiment:
1- les charges FIXES ne concernent que le POIDS PROPRE du plancher en béton armé
2- les charges MOBILES ou CHARGES D'EXPOITATION ne concernent que l'occupation des locaux par les gens
Charges d'exploitation (charges MOBILES)
Commençons par les charges d'exploitation:
Pour la toiture nous allons considérer une charge d'entretien, soit la charge du personnel travaillant sur la toiture pour son
entretien. Cette charge est arrondie par la norme à 1 kN/m²
Pour le plancher du bâtiment pont nous allons considérer une charge de foule. Cette charge est arrondie par la norme à 4
kN/m². En comparaison, dans une chambre, nous considérerons plutôt 1.5 kN/m²
Poids propre (charges PERMANENTES)
En ce qui concerne le poids propre, nous l'avons donc réduit au poids des dalles de béton qui sont portées par les deux grandes poutres treillis (dont nous négligeons à ce stade le poids).
Une méthode de dimensionnement rapide et grossière consiste à diviser la portée d'une dalle par 30 .... 20 pour obtenir son épaisseur. De même pour les poutres on divise par 10.
Nous allons utiliser cette méthode. La portée de ces dalles est de 6m. Divisé par 30 cela fait à peu de choses près 20 cm d'épaisseur de dalle.
Sachant que la densité du béton est de 2.5, soit 2500 kg/m³ ou encore 25 kN/m³
Il suffit de diviser 25 kN par 100 (on a le poids d'une dalle de béton de 1 cm) et de multiplié le résultat par 20 pour obtenir le poids de la dalle. Ce qui revient à ce calcul:
poids propre de la dalle de béton armé = 25 kN/m³ x 0.2m = 5kN/m²
Synthèse des charges surfaciques sur les différentes plateaux
De la charge surfacique à la charge linéaire

La charge linéaire pl reprise dans nos équations d'équilibre correspond à la charge du bâtiment-pont par unité de longueur (par m).
C'est la charge d'une tranche de batiment d'1 m, comme représenté dans la zone en surbrillance sur le schéma ci-contre.
Jusque-là nous avons des charges surfaciques. Pour les transformer en charges linéaires il nous suffit de les multiplier par la largeur du bâtiment-pont.
La charge linéaire pl vaut donc la somme des charges fixes et mobiles soit
6kN/m² x 6m (charges fixes) + 5kN/m² x 6m (charges mobiles) = 66 kN/m

Exercice:
1- Déterminer une chage linéaire
Maintenant que pl est connu, nous pouvons enfin déterminer N!
Reprenons le résultat de nos équations d'équilibre:
R2v = pl x 10.46 m
et
N = R2v / sinus 45°
-> R2v = 66 kN/m x 10.46 m = 690.46 kN
-> N = 690.46 / sin 45° = 976.31 kN
N = 976.31 kN

Maintenant que la sollicitation est connue, comment déterminer le diamètre du tirant?


